LLMs have made remarkable progress in various fields, including natural language processing, question answering, and creative tasks, even demonstrating the ability to solve mathematical problems. Recently, OpenAI’s o1 model, which uses CoT (Chain of Thought), has shown significant reasoning capabilities. However, for a long time, the commonly used GSM8K dataset has had a fixed set of questions and a single evaluation metric, which doesn’t fully capture the models’ abilities. Moreover, due to the popularity of GSM8K, there may be data contamination issues, leading to overly optimistic evaluation results. At the same time, it is difficult to assess the impact of varying problem difficulty on model performance due to a lack of controllability.
Apple researchers aim to address this by developing a more general, adaptive evaluation framework to resolve the reliability issues of current GSM8K evaluation results and explore the factors influencing performance variation. This framework will investigate whether LLMs genuinely understand mathematical concepts and their limitations in dealing with irrelevant information and solving more complex math problems.
Let’s first take a quick look at the article’s conclusions:
To conclude the mathematical reasoning capabilities of large language models, the researchers evaluated over 20 open-source models of various sizes, ranging from 2B to 27B parameters. They evaluated common series such as the Gemma series, Mistral series, Llama3 series, GPT-4o series, Phi series, and models like OpenAI’s recently released o1-mini and o1-preview. Through extensive experiments on these models using the GSM8K and GSM-Symbolic datasets, the authors arrived at the following conclusions:
- The reasoning process of LLMs may not be actual logical reasoning but rather complex pattern matching.
Reasons include a) LLM performance shows significant variance between different instances of the same problem, even when those instances differ only in name or numerical values, and b) LLM performance declines as problem difficulty increases, with performance gaps widening. - LLMs struggle with handling irrelevant information.
LLM performance significantly drops when presented with seemingly related but irrelevant statements in a problem. Even when multiple examples of the same problem or similar irrelevant information are provided, LLMs still need help with these challenges. LLMs need a true understanding of mathematical concepts and the ability to identify relevant information for problem-solving.
Methodology Design
New technical approaches must be developed to conduct a deeper evaluation of LLMs’ mathematical reasoning capabilities. For this reason, researchers at Apple have created a new benchmark:
GSM-Symbolic
GSM-Symbolic is generated from symbolic templates, creating various variants of GSM8K problems. This enables more detailed and reliable evaluations, surpassing the single-point accuracy metric.


GSM-Symbolic Template Creation Process
The design process for GSM-Symbolic is as follows:
- Select a specific example from the GSM8K test set as the template base.
- Parse the example problem into a parsable template:
· Identify the variables in the problem. For example, in the figure above, “Sophie,” “nephew,” “31,” “8,” “9,” and “62” are all variables.
· Define domains for each variable. For instance, “name” can be sampled from a list of common names, and “family” can be “nephew,” “cousin,” or “brother.”
· Add necessary conditions to ensure the correctness of the problem and solution. For example, ensure that all involved numbers are divisible so the solution yields an integer. - Automate checks to ensure annotation correctness:
· Ensure the template does not contain original variable values.
· Ensure original values satisfy all conditions.
· Ensure the generated solution matches the original problem’s solution. - Manually review generated templates: Randomly select ten samples for manual review to ensure template quality.
- The final automated check after all models are evaluated is to ensure that at least two models can correctly answer each question; otherwise, conduct another manual review.
This process allows GSM-Symbolic to generate numerous problem instances and adjust the difficulty as needed. This allows researchers to evaluate LLMs’ mathematical reasoning capabilities more comprehensively and understand their performance in various situations. The resulting GSM-Symbolic dataset contains 100 templates, with 50 samples generated per template, totaling 5,000 examples.
In addition to GSM-Symbolic, the research team also created the
GSM-NoOp dataset.
Its purpose is to challenge the reasoning capabilities of large language models (LLMs) and reveal their limitations in truly understanding mathematical concepts and identifying relevant information for problem-solving.


The creation method of GSM-NoOp is based on the GSM-Symbolic template, adding statements that seem relevant but have no impact on the reasoning process or final answer. These statements are called “No-Op” (no operation) sentences, which don’t involve any real mathematical operations. For example, in the figure above, the problem mentions, “but five of them were a bit smaller than average,” which is irrelevant to calculating the total number of kiwis Oliver has. However, many models incorrectly convert this irrelevant information into a subtraction operation, resulting in an incorrect final answer.
Evaluation Method
For the GSM-Symbolic and GSM-NoOp datasets, the 8-shot CoT (Chain-of-Thought) prompting and greedy decoding methods are used for evaluation.
- 8-shot CoT prompting: Provide 8 example problems and solutions (including full reasoning steps) to guide the model in learning how to solve similar problems.
- Greedy decoding: At each step, the most probable word is selected as the output to generate the final answer.
The main focus for GSM-Symbolic is on model accuracy and distribution across different problem variants.
For GSM-NoOp, the focus is on model accuracy on problems with No-Op sentences, and these results are compared with those from the GSM-Symbolic dataset.
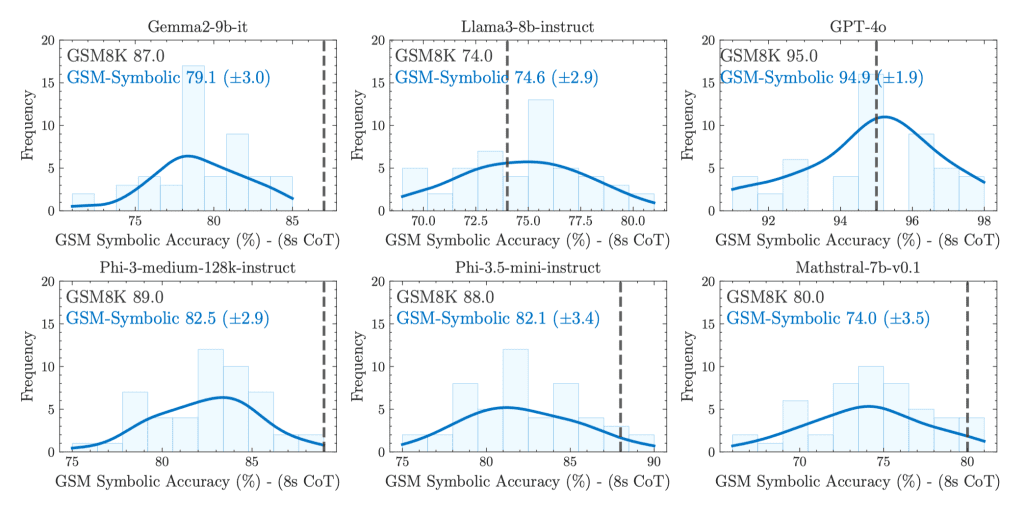


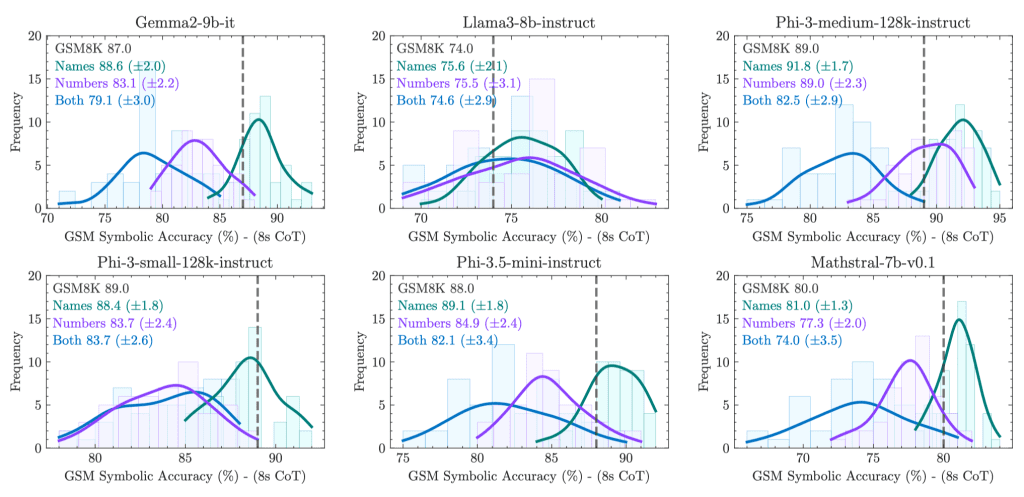

GSM-Symbolic Dataset:
Performance variation: All models exhibit significant performance variation across different problem instances, even if these instances only differ in names or numerical values.
Performance decline: As problem difficulty increases (e.g., by increasing the number of clauses in the problem), LLM performance declines, and performance variation also increases.
GSM-NoOp Dataset:
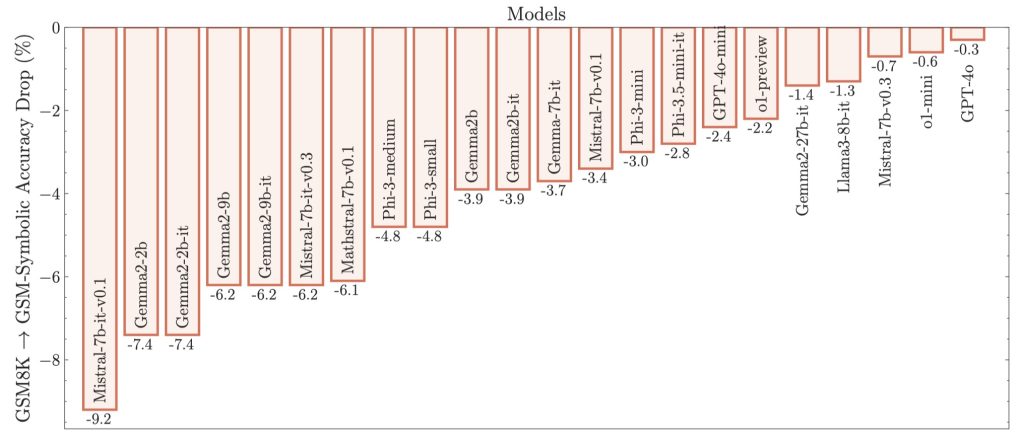
Significant performance decline: All models’ performance declined significantly in the GSM-NoOp dataset, indicating that LLMs struggle with handling irrelevant information and identifying the necessary information to solve problems.
On GSM-NoOp, model performance declines significantly, with newer models showing greater drops than older models. See (a) in the picture below.
Models’ performance on GSM-Symbolic is close to GSM8K. However, on GSM-NoOp, the significant performance decline cannot be recovered. See (b) in the picture below.
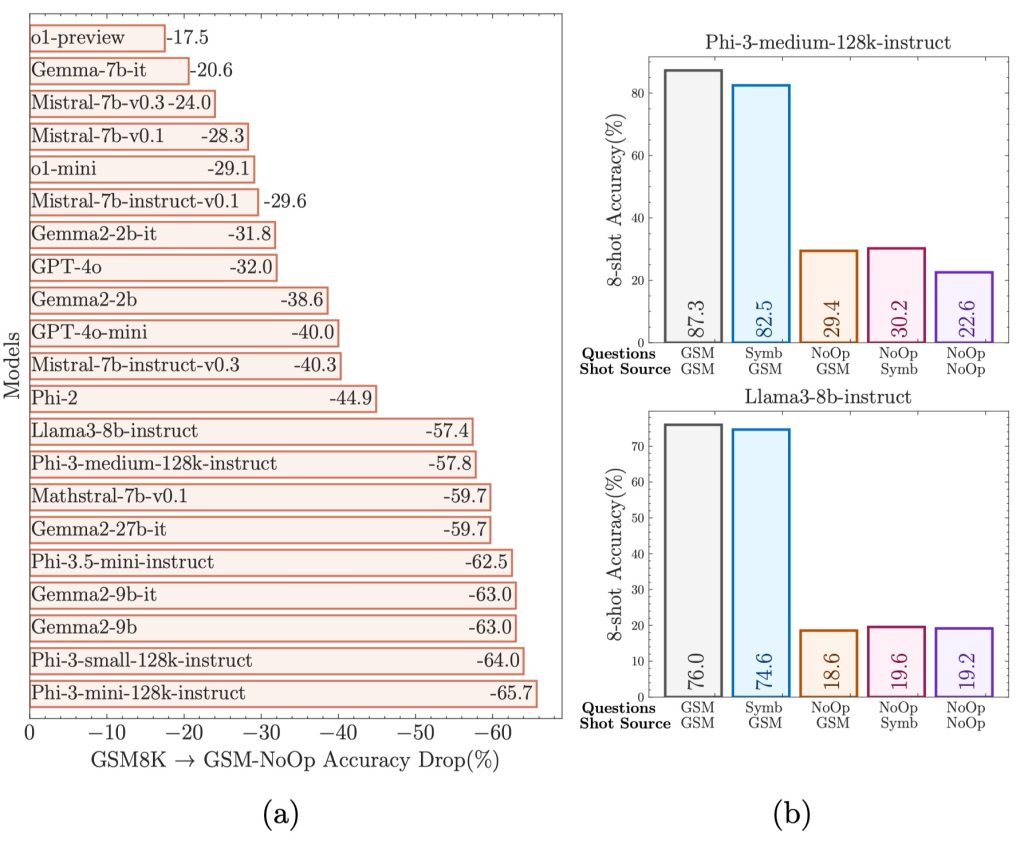

GSM-NoOp adds seemingly related but irrelevant clauses to the GSM-Symbolic template. All models, including the o1 model, show significant performance declines. This indicates that even powerful models like o1 do not truly understand the logical structure of mathematical problems.
Difficult to resolve with few-shot learning or fine-tuning: Even when provided with multiple examples of the same problem or similar irrelevant information, LLMs still struggle to overcome the challenges posed by the GSM-NoOp dataset.
Analysis of o1-preview and o1-mini
While o1-preview and o1-mini outperform other open-source models in overall performance, they still share similar limitations with other models.
On the GSM-Symbolic dataset, o1-preview shows strong robustness, maintaining high accuracy and low-performance variation across different difficulty levels. However, as problem difficulty increases, o1-mini’s accuracy declines, and performance variation increases.
On the GSM-NoOp dataset, o1-mini also shows a significant performance drop, indicating it struggles with handling irrelevant information and identifying key information for solving problems. o1-preview also shows a significant decline, indicating it struggles with fully understanding mathematical concepts and distinguishing relevant information.
The authors provide related examples in the appendix. When dealing with irrelevant information, the o1 model tends to mechanically apply specific operations without truly understanding their meaning. For instance, in one GSM-NoOp problem, even though the donation amount mentioned in the problem is unrelated to the price difference to be solved, the model incorrectly applied a subtraction operation on the donation amount.
Conclusion
In summary, while LLMs have made impressive progress in many areas, their mathematical reasoning capabilities still have significant limitations. Future research should explore new methods to help LLMs learn true mathematical concepts and logical reasoning abilities rather than relying solely on pattern matching. More research and exploration are needed to develop AI systems capable of human-level mathematical reasoning.
Click here to see the research page.